We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Under sufficiently strong assumptions about the first term in an arithmetic progression, we prove that for any integer 
$a$, there are infinitely many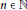 
$n\,\in \,\mathbb{N}$ such that for each prime factor 
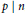$p\,\text{ }\!\!|\!\!\text{ }\,n$, we have 
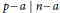$p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers 
$n$ such that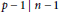 
$p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every 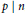$p\,\text{ }\!\!|\!\!\text{ }\,n$.
