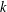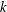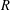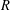Let  $E$ be an elliptic curve over
$E$ be an elliptic curve over  $\mathbb{Q}$ without complex multiplication, and for each prime
$\mathbb{Q}$ without complex multiplication, and for each prime  $p$ of good reduction, let
$p$ of good reduction, let  ${{n}_{E}}(p)\,=\,\left| E\left( {{\mathbb{F}}_{p}} \right) \right|$. For any integer
${{n}_{E}}(p)\,=\,\left| E\left( {{\mathbb{F}}_{p}} \right) \right|$. For any integer  $b$, we consider elliptic pseudoprimes to the base
$b$, we consider elliptic pseudoprimes to the base  $b$. More precisely, let
$b$. More precisely, let  ${{Q}_{E,B}}(x)$ be the number of primes
${{Q}_{E,B}}(x)$ be the number of primes  $p\le x$ such that
$p\le x$ such that  ${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$, and let
${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$, and let  $\pi _{E,b}^{\text{pseu}}(x)$ be the number of compositive
$\pi _{E,b}^{\text{pseu}}(x)$ be the number of compositive ${{n}_{E}}(p)$ such that
${{n}_{E}}(p)$ such that  ${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$ (also called elliptic curve pseudoprimes). Motivated by cryptography applications, we address the problem of finding upper bounds for
${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$ (also called elliptic curve pseudoprimes). Motivated by cryptography applications, we address the problem of finding upper bounds for  ${{Q}_{E,B}}(x)$ and
${{Q}_{E,B}}(x)$ and  $\pi _{E,b}^{\text{pseu}}(x)$, generalising some of the literature for the classical pseudoprimes to this new setting.
$\pi _{E,b}^{\text{pseu}}(x)$, generalising some of the literature for the classical pseudoprimes to this new setting.
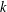 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE