It is shown that simplicity of the crossed product of a unital 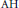 $\text{AH}$-algebra with slow dimension growth by an endomorphism implies that the algebra is also purely infinite, provided only that the endomorphism leaves no trace state invariant and takes the unit to a full projection.
$\text{AH}$-algebra with slow dimension growth by an endomorphism implies that the algebra is also purely infinite, provided only that the endomorphism leaves no trace state invariant and takes the unit to a full projection.