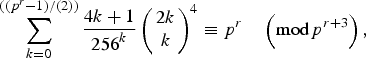1 results
Some congruences involving fourth powers of central q-binomial coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1127-1138
- Print publication:
- June 2020
-
- Article
- Export citation
-
We prove some congruences on sums involving fourth powers of central q-binomial coefficients. As a conclusion, we confirm the following supercongruence observed by Long [Pacific J. Math. 249 (2011), 405–418]:
where p⩾5 is a prime and r is a positive integer. Our method is similar to but a little different from the WZ method used by Zudilin to prove Ramanujan-type supercongruences.
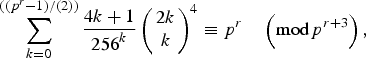$$\sum\limits_{k = 0}^{((p^r-1)/(2))} {\displaystyle{{4k + 1} \over {{256}^k}}} \left( \matrix{2k \cr k} \right)^4\equiv p^r\quad \left( {\bmod p^{r + 3}} \right),$$
