Many connections and dualities in representation theory and Lie theory can be explained using quasi-hereditary covers in the sense of Rouquier. Recent work by the first-named author shows that relative dominant (and codominant) dimensions are natural tools to classify and distinguish distinct quasi-hereditary covers of a finite-dimensional algebra. In this paper, we prove that the relative dominant dimension of a quasi-hereditary algebra, possessing a simple preserving duality, with respect to a direct summand of the characteristic tilting module is always an even number or infinite and that this homological invariant controls the quality of quasi-hereditary covers that possess a simple preserving duality. To resolve the Temperley–Lieb algebras, we apply this result to the class of Schur algebras $S(2, d)$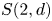 and their $q$
and their $q$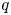 -analogues. Our second main result completely determines the relative dominant dimension of $S(2, d)$
-analogues. Our second main result completely determines the relative dominant dimension of $S(2, d)$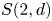 with respect to $Q=V^{\otimes d}$
with respect to $Q=V^{\otimes d}$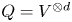 , the $d$
, the $d$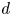 -th tensor power of the natural two-dimensional module. As a byproduct, we deduce that Ringel duals of $q$
-th tensor power of the natural two-dimensional module. As a byproduct, we deduce that Ringel duals of $q$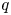 -Schur algebras $S(2,d)$
-Schur algebras $S(2,d)$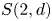 give rise to quasi-hereditary covers of Temperley–Lieb algebras. Further, we obtain precisely when the Temperley–Lieb algebra is Morita equivalent to the Ringel dual of the $q$
give rise to quasi-hereditary covers of Temperley–Lieb algebras. Further, we obtain precisely when the Temperley–Lieb algebra is Morita equivalent to the Ringel dual of the $q$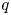 -Schur algebra $S(2, d)$
-Schur algebra $S(2, d)$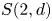 and precisely how far these two algebras are from being Morita equivalent, when they are not. These results are compatible with the integral setup, and we use them to deduce that the Ringel dual of a $q$
and precisely how far these two algebras are from being Morita equivalent, when they are not. These results are compatible with the integral setup, and we use them to deduce that the Ringel dual of a $q$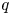 -Schur algebra over the ring of Laurent polynomials over the integers together with some projective module is the best quasi-hereditary cover of the integral Temperley–Lieb algebra.
-Schur algebra over the ring of Laurent polynomials over the integers together with some projective module is the best quasi-hereditary cover of the integral Temperley–Lieb algebra.