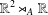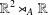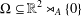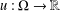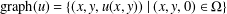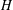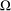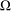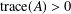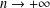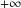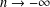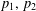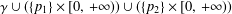In the ambient space of a semidirect product 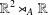 $\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$, we consider a connected domain
$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$, we consider a connected domain 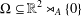 ${\rm\Omega}\subseteq \mathbb{R}^{2}\rtimes _{A}\{0\}$. Given a function
${\rm\Omega}\subseteq \mathbb{R}^{2}\rtimes _{A}\{0\}$. Given a function 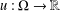 $u:{\rm\Omega}\rightarrow \mathbb{R}$, its
$u:{\rm\Omega}\rightarrow \mathbb{R}$, its  ${\it\pi}$-graph is
${\it\pi}$-graph is 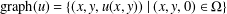 $\text{graph}(u)=\{(x,y,u(x,y))\mid (x,y,0)\in {\rm\Omega}\}$. In this paper we study the partial differential equation that
$\text{graph}(u)=\{(x,y,u(x,y))\mid (x,y,0)\in {\rm\Omega}\}$. In this paper we study the partial differential equation that  $u$ must satisfy so that
$u$ must satisfy so that  $\text{graph}(u)$ has prescribed mean curvature
$\text{graph}(u)$ has prescribed mean curvature 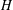 $H$. Using techniques from quasilinear elliptic equations we prove that if a
$H$. Using techniques from quasilinear elliptic equations we prove that if a  ${\it\pi}$-graph has a nonnegative mean curvature function, then it satisfies some uniform height estimates that depend on
${\it\pi}$-graph has a nonnegative mean curvature function, then it satisfies some uniform height estimates that depend on 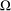 ${\rm\Omega}$ and on the supremum the function attains on the boundary of
${\rm\Omega}$ and on the supremum the function attains on the boundary of 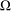 ${\rm\Omega}$. When
${\rm\Omega}$. When 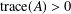 $\text{trace}(A)>0$, we prove that the oscillation of a minimal graph, assuming the same constant value
$\text{trace}(A)>0$, we prove that the oscillation of a minimal graph, assuming the same constant value  $n$ along the boundary, tends to zero when
$n$ along the boundary, tends to zero when 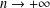 $n\rightarrow +\infty$ and goes to
$n\rightarrow +\infty$ and goes to 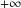 $+\infty$ if
$+\infty$ if 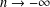 $n\rightarrow -\infty$. Furthermore, we use these estimates, allied with techniques from Killing graphs, to prove the existence of minimal
$n\rightarrow -\infty$. Furthermore, we use these estimates, allied with techniques from Killing graphs, to prove the existence of minimal  ${\it\pi}$-graphs assuming the value zero along a piecewise smooth curve
${\it\pi}$-graphs assuming the value zero along a piecewise smooth curve  ${\it\gamma}$ with endpoints
${\it\gamma}$ with endpoints 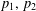 $p_{1},\,p_{2}$ and having as boundary
$p_{1},\,p_{2}$ and having as boundary 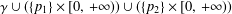 ${\it\gamma}\cup (\{p_{1}\}\times [0,\,+\infty ))\cup (\{p_{2}\}\times [0,\,+\infty ))$.
${\it\gamma}\cup (\{p_{1}\}\times [0,\,+\infty ))\cup (\{p_{2}\}\times [0,\,+\infty ))$.
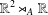 $\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS
$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS