Let T and S be quasisimilar operators on a Banach space X. A well-known result of Herrero shows that each component of the essential spectrum of T meets the essential spectrum of S. Herrero used that, for an n-multicyclic operator, the components of the essential resolvent set with maximal negative index are simply connected. We give new and conceptually simpler proofs for both of Herrero's results based on the observation that on the essential resolvent set of T the section spaces of the sheaves

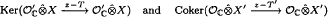
are complete nuclear spaces that are topologically dual to each other. Other concrete applications of this result are given.

Let f be a function in H∞. We show that if f is inner or if the commutant of the analytic Toeplitz operator Tf is equal to that of Tb for some finite Blaschke product b, then any analytic Toeplitz operator quasisimilar to Tf is unitarily equivalent to Tf.

In this article we give a sufficient condition for quasisimilar analytic Toeplitz operators to be unitarily equivalent. We also use a result of Deddens and Wong to give a sufficient condition for an operator intertwining two analytic Toeplitz operators to intertwine their inner parts too. Analytic Toeplitz operators with univalent symbols satisfying a suitable normalization that are quasisimilar are shown to have equal symbols.

Let S be a subnormal operator and let be the weak-star closed algebra generated by S and 1. An example of an irreducible cyclic subnormal operator S is found such that there is a T in with S and T quasisimilar but not unitarily equivalent. However, if S is the unilateral shift, T ∈ and S and T are quasisimilar, then S ≅ T.