We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We present a complete characterisation of the radial asymptotics of degree-one Mahler functions as 
$z$ approaches roots of unity of degree 
$k^{n}$, where 
$k$ is the base of the Mahler function, as well as some applications concerning transcendence and algebraic independence. For example, we show that the generating function of the Thue–Morse sequence and any Mahler function (to the same base) which has a nonzero Mahler eigenvalue are algebraically independent over 
$\mathbb{C}(z)$. Finally, we discuss asymptotic bounds towards generic points on the unit circle.
In this short note, considering functions, we show that taking an asymptotic viewpoint allows one to prove strong transcendence statements in many general situations. In particular, as a consequence of a more general result, we show that if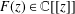 
$F(z)\in \mathbb{C}[[z]]$ is a power series with coefficients from a finite set, then 
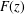$F(z)$ is either rational or it is transcendental over the field of meromorphic functions.
