We consider, for t in the boundary of a Galton–Watson tree $(\partial \textsf{T})$, the covering number $(\textsf{N}_n(t))$ by the generation-n cylinder. For a suitable set I and sequence (sn), we almost surely establish the Hausdorff dimension of the set $\{ t \in \partial {\textsf{T}}:{{\textsf{N}}_n}(t) - nb \ {\sim} \ {s_n}\} $ for b ∈ I.

We consider the generalized version in continuous time of the parking problem of Knuth introduced in Bansaye (2006). Files arrive following a Poisson point process and are stored on a hardware identified with the real line, at the right of their arrival point. Here we study the evolution of the endpoints of the data block straddling 0, which is empty at time 0 and is equal to R at a deterministic time.

Silverman and Brown (1978) have derived Poisson limit theorems for certain sequences of symmetric statistics, based on a sample of independent identically distributed random variables. In this paper an incomplete version of these statistics is considered and a Poisson limit result shown to hold. The powers of some tests based on the incomplete statistic are investigated and the main results of the paper are used to simplify the derivations of the asymptotic distributions of some statistics previously published in the literature.

We showed in [2] that if an object of initial size x (x large) is subjected to a succession of random partitions, then the object is decomposed into a large number of terminal cells, each of relatively small size, where if Z(x, B) denotes the number of such cells whose sizes are points in the set B, then there exists c, (0 < ≦ 1), such that Z(x, B)x−c converges in probability, as x → ∞, to a random variable W. We show here that if a parent object of size x produces k offspring of sizes y1, y2, ···, yk and if for each k x - y1 - y2 - ··· - yk (the ‘waste’ or the ‘cover’, depending on the point of view) is relatively small, then for each n the nth cumulant, Ψn (x, B), of Z(x, B) satisfies Ψn (x, B)x-c → κn (B), as x → ∞, for some κn(B). Thus, writing N = xc, Z(x, B) has approximately the same distribution as the sum of N independent and identically distributed random variables 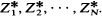(The determination of the distribution of the individual 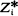appears to be a difficult problem.) The theory also applies when an object of moderate size is broken down into very fine particles or granules.