We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the eigenvalue problem $$ \begin{array}{l}\displaystyle-{\rm div} (a(|\nabla u |)\nabla u) = \lambda g(x, u) \;\mbox{in } \Omega u = 0\;\mbox{on } \partial\Omega ,\end{array}$$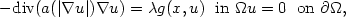 
in the case where the principal operator has rapid growth. By using a variational approach, we show that under certain conditions, almost all λ > 0 are eigenvalues.
