In this paper we investigate analytic affine control systems \hbox{$\dot{q}$}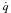 q̇ = X + uY, u ∈ [a,b] , whereX,Y is an orthonormal frame for a generalized Martinet sub-Lorentzianstructure of order k of Hamiltonian type. We construct normal forms forsuch systems and, among other things, we study the connection between the presence of thesingular trajectory starting at q0 on the boundary of thereachable set from q0 with the minimal number of analyticfunctions needed for describing the reachable set from q0.
q̇ = X + uY, u ∈ [a,b] , whereX,Y is an orthonormal frame for a generalized Martinet sub-Lorentzianstructure of order k of Hamiltonian type. We construct normal forms forsuch systems and, among other things, we study the connection between the presence of thesingular trajectory starting at q0 on the boundary of thereachable set from q0 with the minimal number of analyticfunctions needed for describing the reachable set from q0.