We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
An edge flipping is a non-reversible Markov chain on a given connected graph, as defined in Chung and Graham (2012). In the same paper, edge flipping eigenvalues and stationary distributions for some classes of graphs were identified. We further study edge flipping spectral properties to show a lower bound for the rate of convergence in the case of regular graphs. Moreover, we show by a coupling argument that a cutoff occurs at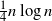 
$\frac{1}{4} n \log n$ for the edge flipping on the complete graph.
