We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We introduce a new kind of action of a relatively hyperbolic group on a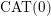 
$\text{CAT}(0)$ cube complex, called a relatively geometric action. We provide an application to characterize finite-volume Kleinian groups in terms of actions on cube complexes, analogous to the results of Markovic and Haïssinsky in the closed case.
