Let G be a countable residually finite group (for instance, 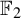 ${\mathbb F}_2$) and let
${\mathbb F}_2$) and let 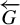 $\overleftarrow {G}$ be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. For every
$\overleftarrow {G}$ be a totally disconnected metric compactification of G equipped with the action of G by left multiplication. For every 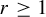 $r\geq 1$, we construct a Toeplitz G-subshift
$r\geq 1$, we construct a Toeplitz G-subshift 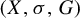 $(X,\sigma ,G)$, which is an almost one-to-one extension of
$(X,\sigma ,G)$, which is an almost one-to-one extension of 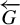 $\overleftarrow {G}$, having r ergodic measures
$\overleftarrow {G}$, having r ergodic measures  $\nu _1, \ldots ,\nu _r$ such that for every
$\nu _1, \ldots ,\nu _r$ such that for every 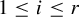 $1\leq i\leq r$, the measure-theoretic dynamical system
$1\leq i\leq r$, the measure-theoretic dynamical system 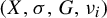 $(X,\sigma ,G,\nu _i)$ is isomorphic to
$(X,\sigma ,G,\nu _i)$ is isomorphic to 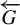 $\overleftarrow {G}$ endowed with the Haar measure. The construction we propose is general (for amenable and non-amenable residually finite groups); however, we point out the differences and obstructions that could appear when the acting group is not amenable.
$\overleftarrow {G}$ endowed with the Haar measure. The construction we propose is general (for amenable and non-amenable residually finite groups); however, we point out the differences and obstructions that could appear when the acting group is not amenable.