We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the relative Donaldson–Thomas theory of 𝒜n×P1, where 𝒜n is the surface resolution of type An singularity. The action of divisor operators in the theory is expressed in terms of operators of the affine algebra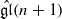 
on Fock space. Assuming a nondegeneracy conjecture, this gives a complete solution for the theory. The results complete the comparison of this theory with the Gromov–Witten theory of 𝒜n×P1 and the quantum cohomology of the Hilbert scheme of points on 𝒜n.
