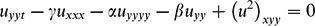1 results
Analysis of 2 + 1 diffusive–dispersive PDE arising in river braiding
-
- Journal:
- European Journal of Applied Mathematics / Volume 27 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 16 February 2016, pp. 756-780
-
- Article
- Export citation
-
We present local existence and uniqueness results for the following 2 + 1 diffusive–dispersive equation due to P. Hall arising in modelling of river braiding:
for (x,y) ∈ [0, 2π] × [0, π], t > 0, with boundary condition uy=0=uyyy at y=0 and y=π and 2π periodicity in x, using a contraction mapping argument in a Bourgain-type space Ts,b. We also show that the energy ∥u(·, ·, t)∥2L2 and cumulative dissipation ∫0t∥uy (·, ·, s)∥L22dt are globally controlled in time t.
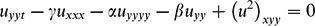$$\begin{equation*}
u_{yyt} - \gamma u_{xxx} -\alpha u_{yyyy} - \beta u_{yy} + \left ( u^2 \right )_{xyy} = 0 \end{equation*}$$
