We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We obtain a complete topological classification of $k$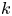
-folding map-germs on generic surfaces in $\mathbb {R}^3$
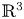, discover new robust features of surfaces and recover, in a unified way, many of the robust features that were obtained previously by considering the contact of a surface with lines, planes or spheres.
