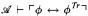Refine search
Actions for selected content:
9 results
ON THE CATEGORICITY OF COMPLETE SECOND-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-23
-
- Article
- Export citation

Philosophical Uses of Categoricity Arguments
-
- Published online:
- 02 December 2023
- Print publication:
- 21 December 2023
-
- Element
- Export citation
TWO-SORTED FREGE ARITHMETIC IS NOT CONSERVATIVE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1199-1232
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEDUCTIVE CARDINALITY RESULTS AND NUISANCE-LIKE PRINCIPLES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 April 2021, pp. 592-623
- Print publication:
- September 2021
-
- Article
- Export citation
A NOTE ON CHOICE PRINCIPLES IN SECOND-ORDER LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 August 2020, pp. 339-350
- Print publication:
- June 2023
-
- Article
- Export citation
AN EXTENSION OF A THEOREM OF ZERMELO
-
- Journal:
- Bulletin of Symbolic Logic / Volume 25 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 06 March 2019, pp. 208-212
- Print publication:
- June 2019
-
- Article
- Export citation
CAPTURING CONSEQUENCE
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 March 2019, pp. 271-295
- Print publication:
- June 2019
-
- Article
- Export citation
ISOMORPHISM INVARIANCE AND OVERGENERATION
-
- Journal:
- Bulletin of Symbolic Logic / Volume 22 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 30 December 2016, pp. 482-503
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Frege's unofficial arithmetic
-
- Journal:
- The Journal of Symbolic Logic / Volume 67 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1623-1638
- Print publication:
- December 2002
-
- Article
- Export citation




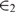

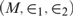
 of
of  of
of 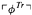 is a second-order sentence containing no arithmetical vocabulary, and
is a second-order sentence containing no arithmetical vocabulary, and