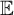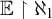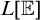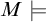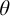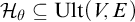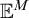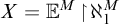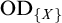Refine search
Actions for selected content:
1 results
THE DEFINABILITY OF THE EXTENDER SEQUENCE
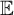 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 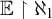 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 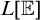 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation