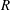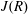1 results
Rings whose Elements are the Sum of a Tripotent and an Element from the Jacobson Radical
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 March 2019, pp. 810-821
- Print publication:
- December 2019
-
- Article
- Export citation
-
This paper is about rings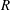
$R$ for which every element is a sum of a tripotent and an element from the Jacobson radical 
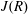$J(R)$. These rings are called semi-tripotent rings. Examples include Boolean rings, strongly nil-clean rings, strongly 2-nil-clean rings, and semi-boolean rings. Here, many characterizations of semi-tripotent rings are obtained. Necessary and sufficient conditions for a Morita context (respectively, for a group ring of an abelian group or a locally finite nilpotent group) to be semi-tripotent are proved.
