We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the problem of counting the number of rational points of bounded height in the zero-loci of Brauer group elements on semi-simple algebraic groups over number fields. We obtain asymptotic formulae for the counting problem for wonderful compactifications using the spectral theory of automorphic forms. Applications include asymptotic formulae for the number of matrices over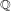 
$\mathbb{Q}$ whose determinant is a sum of two squares. These results provide a positive answer to some cases of a question of Serre concerning such counting problems.
