We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we show the existence of solution for the following class of semipositone problem
P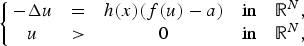
where N ≥ 3, a > 0, h : ℝN → (0, + ∞) and f : [0, + ∞) → [0, + ∞) are continuous functions with f having a subcritical growth. The main tool used is the variational method together with estimates that involve the Riesz potential.
$$\left\{\matrix{-\Delta u & = & h(x)(f(u)-a) & \hbox{in} & {\open R}^N, \cr u & \gt & 0 & \hbox{in} & {\open R}^N, \cr}\right.$$
