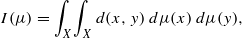The formulation of optimal reinsurance policies that take various practical constraints into account is a problem commonly encountered by practitioners. In the context of a distortion-risk-measure-based optimal reinsurance model without moral hazard, this article introduces and employs a variation of the Neyman–Pearson Lemma in statistical hypothesis testing theory to solve a wide class of constrained optimal reinsurance problems analytically and expeditiously. Such a Neyman–Pearson approach identifies the unit-valued derivative of each ceded loss function as the test function of an appropriate hypothesis test and transforms the problem of designing optimal reinsurance contracts to one that resembles the search of optimal test functions achieved by the classical Neyman–Pearson Lemma. As an illustration of the versatility and superiority of the proposed Neyman–Pearson formulation, we provide complete and transparent solutions of several specific constrained optimal reinsurance problems, many of which were only partially solved in the literature by substantially more difficult means and under extraneous technical assumptions. Examples of such problems include the construction of the optimal reinsurance treaties in the presence of premium budget constraints, counterparty risk constraints and the optimal insurer–reinsurer symbiotic reinsurance treaty considered recently in Cai et al. (2016).

Let (X,d) be a compact metric space and let ℳ(X) denote the space of all finite signed Borel measures on X. Define I:ℳ(X)→ℝ by 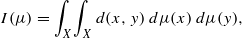and set M(X)=sup I(μ), where μ ranges over the collection of signed measures in ℳ(X) of total mass 1. The metric space (X,d) is quasihypermetric if for all n∈ℕ, all α1,…,αn∈ℝ satisfying ∑ i=1nαi=0 and all x1,…,xn∈X, the inequality ∑ i,j=1nαiαjd(xi,xj)≤0 holds. Without the quasihypermetric property M(X) is infinite, while with the property a natural semi-inner product structure becomes available on ℳ0(X), the subspace of ℳ(X) of all measures of total mass 0. This paper explores: operators and functionals which provide natural links between the metric structure of (X,d), the semi-inner product space structure of ℳ0(X) and the Banach space C(X) of continuous real-valued functions on X; conditions equivalent to the quasihypermetric property; the topological properties of ℳ0(X) with the topology induced by the semi-inner product, and especially the relation of this topology to the weak-* topology and the measure-norm topology on ℳ0(X); and the functional-analytic properties of ℳ0(X) as a semi-inner product space, including the question of its completeness. A later paper [P. Nickolas and R. Wolf, Distance geometry in quasihypermetric spaces. II, Math. Nachr., accepted] will apply the work of this paper to a detailed analysis of the constant M(X).

We present, discuss and prove an apparently unfamiliar result in the convergence of probability measures.