Given a Lie n-algebra, we provide an explicit construction of its integrating Lie n-group. This extends work done by Getzler in the case of nilpotent 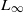 -algebras. When applied to an ordinary Lie algebra, our construction yields the simplicial classifying space of the corresponding simply connected Lie group. In the case of the string Lie 2-algebra of Baez and Crans, we obtain the simplicial nerve of their model of the string group.
-algebras. When applied to an ordinary Lie algebra, our construction yields the simplicial classifying space of the corresponding simply connected Lie group. In the case of the string Lie 2-algebra of Baez and Crans, we obtain the simplicial nerve of their model of the string group.
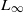 -algebras
-algebras