Search

Summary

This chapter contains a brief introduction to nilmanifolds, and a discussion of Künneth and related structures on nilmanifolds. Nilmanifolds are homogeneous spaces for nilpotent Lie groups, and for them the discussions of geometric structures can often be reduced to the consideration of left-invariant structures. Left-invariant structures in turn arise from the corresponding linear structures on the Lie algebra, and these linear structures are usually much more tractable than arbitrary geometric structures on smooth manifolds. The nilmanifolds of abelian Lie groups are just tori, so that in some sense nilmanifolds are the simplest generalisations of tori.

We do not give a systematic treatment of nilmanifolds here, but focus on providing a few explicit examples of Künneth structures, of hypersymplectic structures, and of Anosov symplectomorphisms in this setting. For more information on topics from the theory of nilmanifolds that we treat rather breezily, we refer to the books by Gorbatsevich, Onishchik and Vinberg [GOV-97] and by Knapp [Kna-96].

We show that closed 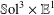$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-manifolds are Seifert fibred, with general fibre the torus, and base one of the flat 2-orbifolds 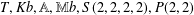$T,Kb,\mathbb{A},\mathbb{M}b,S(2,2,2,2),P(2,2)$ or 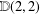$\mathbb{D}(2,2)$, and outline how such manifolds may be classified.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

9 - Nilmanifolds

Summary

$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

9 - Nilmanifolds

Summary

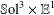$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS