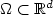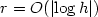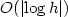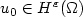Refine search
Actions for selected content:
3 results
A Stochastic Collocation Method for Delay Differential Equations with Random Input
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 4 / August 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 403-418
- Print publication:
- August 2014
-
- Article
- Export citation
A Numerical Comparison Between Quasi-Monte Carlo and Sparse Grid Stochastic Collocation Methods
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1051-1069
- Print publication:
- October 2012
-
- Article
- Export citation
Numerical solution of parabolic equationsin high dimensions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 93-127
- Print publication:
- January 2004
-
- Article
- Export citation