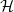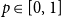Given a hereditary property of graphs $\mathcal{H}$ and a $p\in [0,1]$ , the edit distance function 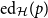$\textrm{ed}_{\mathcal{H}}(p)$ is asymptotically the maximum proportion of edge additions plus edge deletions applied to a graph of edge density p sufficient to ensure that the resulting graph satisfies 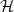$\mathcal{H}$ . 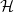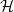The edit distance function is directly related to other well-studied quantities such as the speed function for $\mathcal{H}$ and the $\mathcal{H}$ -chromatic number of a random graph.

Let 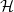$\mathcal{H}$ be the property of forbidding an Erdős–Rényi random graph 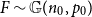$F\sim \mathbb{G}(n_0,p_0)$ , and let 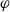$\varphi$ represent the golden ratio. In this paper, we show that if 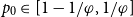$p_0\in [1-1/\varphi,1/\varphi]$ , then a.a.s. as 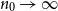$n_0\to\infty$ ,

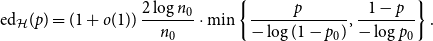\begin{align*} {\textrm{ed}}_{\mathcal{H}}(p) = (1+o(1))\,\frac{2\log n_0}{n_0} \cdot\min\left\{ \frac{p}{-\log(1-p_0)}, \frac{1-p}{-\log p_0} \right\}. \end{align*}

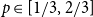$p\in [1/3,2/3]$

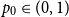$p_0\in (0,1)$

A primary tool in the proof is the categorization of p-core coloured regularity graphs in the range 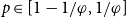$p\in[1-1/\varphi,1/\varphi]$ . Such coloured regularity graphs must have the property that the non-grey edges form vertex-disjoint cliques.

In this paper, a new method is proposed to find a feasible energy-efficient path between an initial point and goal point on uneven terrain and then to optimally traverse the path. The path is planned by integrating the geometric features of the uneven terrain and the biped robot dynamics. This integrated information of biped dynamics and associated cost (energy) for moving toward the goal point is used to define the value of a new speed function at each point on the discretized surface of the terrain. The value is stored as a matrix called the dynamic transport cost (DTC). The path is obtained by solving the Eikonal equation numerically by fast marching method (FMM) on an orthogonal grid, by using the information stored in the DTC matrix. One step of walk on uneven terrain is characterized by 10 footstep parameters (FSPs); these FSPs represent the position of swinging foot at the starting and ending time of the walk, orientation, and state (left or right) of support foot. A walking dataset was created for different walking conditions (FSPs), which the biped robot is likely to encounter when it has to walk on the uneven terrain. The corresponding energy optimal hip and foot trajectory parameters (HFTPs) are obtained by optimization using a genetic algorithm (GA). The created walk dataset is generalized by training a feedforward neural network (NN) using the scaled conjugate gradient (SCG) algorithm. The Foot placement planner gives a sequence of foot positions and orientations along the obtained path, which is followed by the biped robot by generating real-time optimal foot and hip trajectories using the learned NN. Simulation results on different types of uneven terrains validate the proposed method.