We show that the Mallows measure on permutations of $1,\dots ,n$ arises as the law of the unique Gale–Shapley stable matching of the random bipartite graph with vertex set conditioned to be perfect, where preferences arise from the natural total ordering of the vertices of each gender but are restricted to the (random) edges of the graph. We extend this correspondence to infinite intervals, for which the situation is more intricate. We prove that almost surely, every stable matching of the random bipartite graph obtained by performing Bernoulli percolation on the complete bipartite graph $K_{{\mathbb Z},{\mathbb Z}}$ falls into one of two classes: a countable family $(\sigma _n)_{n\in {\mathbb Z}}$ of tame stable matchings, in which the length of the longest edge crossing k is $O(\log |k|)$ as 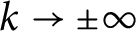$k\to \pm \infty $ , and an uncountable family of wild stable matchings, in which this length is $\exp \Omega (k)$ as $k\to +\infty $ . The tame stable matching $\sigma _n$ has the law of the Mallows permutation of ${\mathbb Z}$ (as constructed by Gnedin and Olshanski) composed with the shift $k\mapsto k+n$ . The permutation $\sigma _{n+1}$ dominates $\sigma _{n}$ pointwise, and the two permutations are related by a shift along a random strictly increasing sequence.

Suppose that red and blue points occur in Rd according to two simple point processes with finite intensities λR and λB, respectively. Furthermore, let ν and μ be two probability distributions on the strictly positive integers with means ν̅ and μ̅, respectively. Assign independently a random number of stubs (half-edges) to each red (blue) point with law ν (μ). We are interested in translation-invariant schemes for matching stubs between points of different colors in order to obtain random bipartite graphs in which each point has a prescribed degree distribution with law ν or μ depending on its color. For a large class of point processes, we show that such translation-invariant schemes matching almost surely all stubs are possible if and only if λRν̅ = λBμ̅, including the case when ν̅ = μ̅ = ∞ so that both sides are infinite. Furthermore, we study a particular scheme based on the Gale-Shapley stable marriage problem. For this scheme, we give sufficient conditions on ν and μ for the presence and absence of infinite components. These results are two-color versions of those obtained by Deijfen, Holroyd and Häggström.