Effect size indices are useful tools in study design and reporting because they are unitless measures of association strength that do not depend on sample size. Existing effect size indices are developed for particular parametric models or population parameters. Here, we propose a robust effect size index based on M-estimators. This approach yields an index that is very generalizable because it is unitless across a wide range of models. We demonstrate that the new index is a function of Cohen’s d, \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$R^2$$\end{document}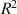 , and standardized log odds ratio when each of the parametric models is correctly specified. We show that existing effect size estimators are biased when the parametric models are incorrect (e.g., under unknown heteroskedasticity). We provide simple formulas to compute power and sample size and use simulations to assess the bias and standard error of the effect size estimator in finite samples. Because the new index is invariant across models, it has the potential to make communication and comprehension of effect size uniform across the behavioral sciences.
, and standardized log odds ratio when each of the parametric models is correctly specified. We show that existing effect size estimators are biased when the parametric models are incorrect (e.g., under unknown heteroskedasticity). We provide simple formulas to compute power and sample size and use simulations to assess the bias and standard error of the effect size estimator in finite samples. Because the new index is invariant across models, it has the potential to make communication and comprehension of effect size uniform across the behavioral sciences.