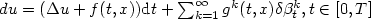In this article, we consider the stochastic heat equation $du=(\Delta u+f(t,x)){\rm d}t+ \sum_{k=1}^{\infty} g^{k}(t,x) \delta \beta_t^k, t \in [0,T]$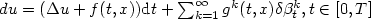, with random coefficients f and gk,driven by a sequence (βk)k of i.i.d. fractional Brownianmotions of index H>1/2. Using the Malliavin calculus techniquesand a p-th moment maximal inequality for the infinite sum ofSkorohod integrals with respect to (βk)k, we prove that theequation has a unique solution (in a Banach space of summabilityexponent p ≥ 2), and this solution is Hölder continuous inboth time and space.

This paper introduces a fractional heat equation, where the diffusion operator is the composition of the Bessel and Riesz potentials. Sharp bounds are obtained for the variance of the spatial and temporal increments of the solution. These bounds establish the degree of singularity of the sample paths of the solution. In the case of unbounded spatial domain, a solution is formulated in terms of the Fourier transform of its spatially and temporally homogeneous Green function. The spectral density of the resulting solution is then obtained explicitly. The result implies that the solution of the fractional heat equation may possess spatial long-range dependence asymptotically.