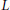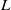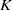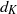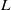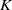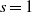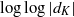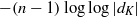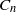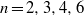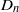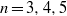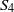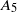Let 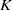 $K$ be a number field of degree
$K$ be a number field of degree  $n$, and let
$n$, and let 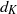 $d_K$ be its discriminant. Then, under the Artin conjecture, the generalized Riemann hypothesis and a certain zero-density hypothesis, we show that the upper and lower bounds of the logarithmic derivatives of Artin
$d_K$ be its discriminant. Then, under the Artin conjecture, the generalized Riemann hypothesis and a certain zero-density hypothesis, we show that the upper and lower bounds of the logarithmic derivatives of Artin 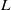 $L$-functions attached to
$L$-functions attached to 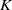 $K$ at
$K$ at 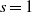 $s=1$ are
$s=1$ are 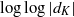 $\log \log |d_K|$ and
$\log \log |d_K|$ and 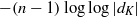 $-(n-1) \log \log |d_K|$, respectively. Unconditionally, we show that there are infinitely many number fields with the extreme logarithmic derivatives; they are families of number fields whose Galois closures have the Galois group
$-(n-1) \log \log |d_K|$, respectively. Unconditionally, we show that there are infinitely many number fields with the extreme logarithmic derivatives; they are families of number fields whose Galois closures have the Galois group 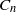 $C_n$ for
$C_n$ for 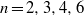 $n=2,3,4,6$,
$n=2,3,4,6$, 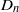 $D_n$ for
$D_n$ for 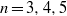 $n=3,4,5$,
$n=3,4,5$, 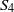 $S_4$ or
$S_4$ or 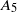 $A_5$.
$A_5$.
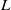 $L$-functions
$L$-functions