We establish that the existence of a winning strategy in certain topological games, closely related to a strong game of Choquet, played in a topological space 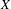 $X$ and its hyperspace
$X$ and its hyperspace 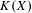 $K(X)$ of all nonempty compact subsets of
$K(X)$ of all nonempty compact subsets of 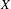 $X$ equipped with the Vietoris topology, is equivalent for one of the players. For a separable metrizable space
$X$ equipped with the Vietoris topology, is equivalent for one of the players. For a separable metrizable space 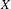 $X$, we identify a game-theoretic condition equivalent to
$X$, we identify a game-theoretic condition equivalent to 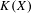 $K(X)$ being hereditarily Baire. It implies quite easily a recent result of Gartside, Medini and Zdomskyy that characterizes hereditary Baire property of hyperspaces
$K(X)$ being hereditarily Baire. It implies quite easily a recent result of Gartside, Medini and Zdomskyy that characterizes hereditary Baire property of hyperspaces 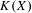 $K(X)$ over separable metrizable spaces
$K(X)$ over separable metrizable spaces 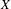 $X$ via the Menger property of the remainder of a compactification of
$X$ via the Menger property of the remainder of a compactification of 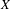 $X$. Subsequently, we use topological games to study hereditary Baire property in spaces of probability measures and in hyperspaces over filters on natural numbers. To this end, we introduce a notion of strong
$X$. Subsequently, we use topological games to study hereditary Baire property in spaces of probability measures and in hyperspaces over filters on natural numbers. To this end, we introduce a notion of strong  $P$-filter
$P$-filter 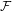 ${\mathcal{F}}$ and prove that it is equivalent to
${\mathcal{F}}$ and prove that it is equivalent to 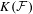 $K({\mathcal{F}})$ being hereditarily Baire. We also show that if
$K({\mathcal{F}})$ being hereditarily Baire. We also show that if 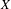 $X$ is separable metrizable and
$X$ is separable metrizable and 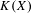 $K(X)$ is hereditarily Baire, then the space
$K(X)$ is hereditarily Baire, then the space 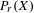 $P_{r}(X)$ of Borel probability Radon measures on
$P_{r}(X)$ of Borel probability Radon measures on 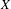 $X$ is hereditarily Baire too. It follows that there exists (in ZFC) a separable metrizable space
$X$ is hereditarily Baire too. It follows that there exists (in ZFC) a separable metrizable space 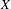 $X$, which is not completely metrizable with
$X$, which is not completely metrizable with 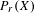 $P_{r}(X)$ hereditarily Baire. As far as we know, this is the first example of this kind.
$P_{r}(X)$ hereditarily Baire. As far as we know, this is the first example of this kind.