1 results
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
Open conjectures state that, for every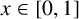
$x\in [0,1]$, the orbit 
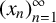$(x_n)_{n=1}^\infty $ of the mean-median recursion 
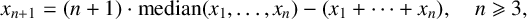$$ \begin{align*}x_{n+1}=(n+1)\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$with initial data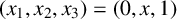
$(x_1,x_2,x_3)=(0,x,1)$, is eventually constant, and that its transit time and limit functions (of x) are unbounded and continuous, respectively. In this paper, we prove that for the slightly modified recursion 
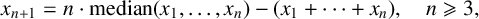$$ \begin{align*}x_{n+1}=n\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$first suggested by Akiyama, the transit time function is unbounded but the limit function is discontinuous.
