1 results
A remark on fullness of some group measure space von Neumann algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 2493-2502
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
-
Recently Houdayer and Isono have proved, among other things, that every biexact group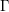
$\unicode[STIX]{x1D6E4}$ has the property that for any non-singular strongly ergodic essentially free action 
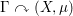$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ on a standard measure space, the group measure space von Neumann algebra 
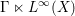$\unicode[STIX]{x1D6E4}\ltimes L^{\infty }(X)$ is full. In this paper, we prove the same property for a wider class of groups, notably including 
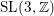$\text{SL}(3,\mathbb{Z})$. We also prove that for any connected simple Lie group 
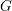$G$ with finite center, any lattice 
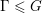$\unicode[STIX]{x1D6E4}\leqslant G$, and any closed non-amenable subgroup 
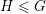$H\leqslant G$, the non-singular action 
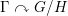$\unicode[STIX]{x1D6E4}\curvearrowright G/H$ is strongly ergodic and the von Neumann factor 
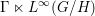$\unicode[STIX]{x1D6E4}\ltimes L^{\infty }(G/H)$ is full.
