1 results
Comparison and existence results for evolutive non-coercive first-order Hamilton-Jacobi equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 3 / July 2007
- Published online by Cambridge University Press:
- 05 June 2007, pp. 484-502
- Print publication:
- July 2007
-
- Article
- Export citation
-
In this paper we prove a comparison result between semicontinuousviscosity subsolutions and supersolutions to Hamilton-Jacobi equations of the form $u_t+H(x,Du) = 0$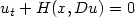
in ${\rm I}\!{\rmR}^n\times(0,T)$ 
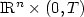where the Hamiltonian H may be noncoercive inthe gradient Du. As a consequence of the comparison result and the Perron's method we get the existence of a continuous solution of this equation.
