1 results
Exponential deficiency of convolutions of densities∗
-
- Journal:
- ESAIM: Probability and Statistics / Volume 16 / 2012
- Published online by Cambridge University Press:
- 02 July 2012, pp. 86-96
- Print publication:
- 2012
-
- Article
- Export citation
-
If a probability density p(x) (x ∈ ℝk) is bounded and R(t) := ∫e〈x, tu〉p(x)dx < ∞ for some linear functional u and all t ∈ (0,1), then, for each t ∈ (0,1) and all large enough n, the n-fold convolution of the t-tilted density \hbox{$\tilde p_t$}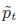
:= e〈x, tu〉p(x)/R(t) is bounded. This is a corollary of a general, “non-i.i.d.” result, which is also shown to enjoy a certain optimality property. Such results and their corollaries stated in terms of the absolute integrability of the corresponding characteristic functions are useful for saddle-point approximations.
