We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We construct a mirabolic analogue of the geometric Satake equivalence. We also prove an equivalence that relates representations of a supergroup to the category of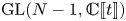 
$\operatorname{GL}(N-1,{\mathbb {C}}[\![t]\!])$-equivariant perverse sheaves on the affine Grassmannian of 
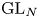$\operatorname{GL}_N$. We explain how our equivalences fit into a more general framework of conjectures due to Gaiotto and to Ben-Zvi, Sakellaridis and Venkatesh.
