1 results
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
-
We study the values of finite multiple harmonic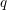
$q$-series at a primitive root of unity and show that these specialize to the finite multiple zeta value (FMZV) and the symmetric multiple zeta value (SMZV) through an algebraic and analytic operation, respectively. Further, we prove the duality formula for these values, as an example of linear relations, which induce those among FMZVs and SMZVs simultaneously. This gives evidence towards a conjecture of Kaneko and Zagier relating FMZVs and SMZVs. Motivated by the above results, we define cyclotomic analogues of FMZVs, which conjecturally generate a vector space of the same dimension as that spanned by the finite multiple harmonic 
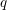$q$-series at a primitive root of unity of sufficiently large degree.
