We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We construct a dynamically convex contact form on the three-sphere whose systolic ratio is arbitrarily close to 2. This example is related to a conjecture of Viterbo, whose validity would imply that the systolic ratio of a convex contact form does not exceed 1. We also construct, for every integer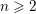 
$n\geqslant 2$, a tight contact form with systolic ratio arbitrarily close to 
$n$ and with suitable bounds on the mean rotation number of all the closed orbits of the induced Reeb flow.
