We construct a new type of planar Euler flows with localized vorticity. Let 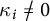$\kappa _i\not =0$ , $i=1,\ldots , m$ , be m arbitrarily fixed constants. For any given nondegenerate critical point 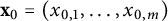$\mathbf {x}_0=(x_{0,1},\ldots ,x_{0,m})$ of the Kirchhoff–Routh function defined on 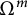$\Omega ^m$ corresponding to $(\kappa _1,\ldots , \kappa _m)$ , we construct a family of stationary planar flows with vortex sheets that have large vorticity amplitude and concentrate on curves perturbed from small circles centered near 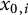$x_{0,i}$ , $i=1,\ldots ,m$ . The proof is accomplished via the implicit function theorem with suitable choice of function spaces.