Let $p_{\{3, 3\}}(n)$ denote the number of $3$ -regular partitions in three colours. Da Silva and Sellers [‘Arithmetic properties of 3-regular partitions in three colours’, Bull. Aust. Math. Soc. 104(3) (2021), 415–423] conjectured four Ramanujan-like congruences modulo $5$ satisfied by $p_{\{3, 3\}}(n)$ . We confirm these conjectural congruences using the theory of modular forms.

Gireesh and Mahadeva Naika [‘On 3-regular partitions in 3-colors’, Indian J. Pure Appl. Math.50 (2019), 137–148] proved an infinite family of congruences modulo powers of 3 for the function 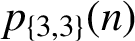$p_{\{3,3\}}(n)$ , the number of 3-regular partitions in three colours. In this paper, using elementary generating function manipulations and classical techniques, we significantly extend the list of proven arithmetic properties satisfied by $p_{\{3,3\}}(n).$