The main theme of this paper is to study 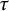 $\tau $-tilting subcategories in an abelian category
$\tau $-tilting subcategories in an abelian category 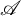 $\mathscr {A}$ with enough projective objects. We introduce the notion of
$\mathscr {A}$ with enough projective objects. We introduce the notion of 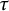 $\tau $-cotorsion torsion triples and investigate a bijection between the collection of
$\tau $-cotorsion torsion triples and investigate a bijection between the collection of 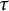 $\tau $-cotorsion torsion triples in
$\tau $-cotorsion torsion triples in 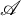 $\mathscr {A}$ and the collection of support
$\mathscr {A}$ and the collection of support 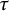 $\tau $-tilting subcategories of
$\tau $-tilting subcategories of 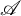 $\mathscr {A}$, generalizing the bijection by Bauer, Botnan, Oppermann, and Steen between the collection of cotorsion torsion triples and the collection of tilting subcategories of
$\mathscr {A}$, generalizing the bijection by Bauer, Botnan, Oppermann, and Steen between the collection of cotorsion torsion triples and the collection of tilting subcategories of 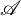 $\mathscr {A}$. General definitions and results are exemplified using persistent modules. If
$\mathscr {A}$. General definitions and results are exemplified using persistent modules. If 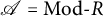 $\mathscr {A}=\mathrm{Mod}\mbox {-}R$, where R is a unitary associative ring, we characterize all support
$\mathscr {A}=\mathrm{Mod}\mbox {-}R$, where R is a unitary associative ring, we characterize all support 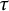 $\tau $-tilting (resp. all support
$\tau $-tilting (resp. all support 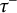 $\tau ^-$-tilting) subcategories of
$\tau ^-$-tilting) subcategories of 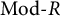 $\mathrm{Mod}\mbox {-}R$ in terms of finendo quasitilting (resp. quasicotilting) modules. As a result, it will be shown that every silting module (resp. every cosilting module) induces a support
$\mathrm{Mod}\mbox {-}R$ in terms of finendo quasitilting (resp. quasicotilting) modules. As a result, it will be shown that every silting module (resp. every cosilting module) induces a support 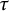 $\tau $-tilting (resp. support
$\tau $-tilting (resp. support 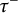 $\tau ^{-}$-tilting) subcategory of
$\tau ^{-}$-tilting) subcategory of 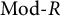 $\mathrm{Mod}\mbox {-}R$. We also study the theory in
$\mathrm{Mod}\mbox {-}R$. We also study the theory in 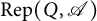 $\mathrm {Rep}(Q, \mathscr {A})$, where Q is a finite and acyclic quiver. In particular, we give an algorithm to construct support
$\mathrm {Rep}(Q, \mathscr {A})$, where Q is a finite and acyclic quiver. In particular, we give an algorithm to construct support 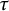 $\tau $-tilting subcategories in
$\tau $-tilting subcategories in 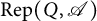 $\mathrm {Rep}(Q, \mathscr {A})$ from certain support
$\mathrm {Rep}(Q, \mathscr {A})$ from certain support 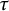 $\tau $-tilting subcategories of
$\tau $-tilting subcategories of 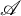 $\mathscr {A}$.
$\mathscr {A}$.