With the general assumption that the manifold admits two orthogonal complementary foliations, one of which is totally geodesic, we study the components of the curvature tensor field of the characteristic connection.
In the case where the manifold is compact, orientable of dimension 6 or 8 and the dimension of the totally geodesic foliation is 4, we relate the sign of the Euler characteristic of the manifold and that of the sectional curvature of the leaves of both foliations.
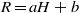 $R= aH+ b$
$R= aH+ b$