We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show how some of the refined tropical counts of Block and Göttsche emerge from the wall-crossing formalism. This leads naturally to a definition of a class of putative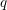 
$q$-deformed Gromov–Witten invariants. We prove that this coincides with another natural 
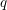$q$-deformation, provided by a result of Reineke and Weist in the context of quiver representations, when the latter is well defined.
