1 results
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We use the tropical geometry approach to compute absolute and relative enumerative invariants of complex surfaces which are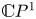
$\mathbb {C} P^1$-bundles over an elliptic curve. We also show that the tropical multiplicity used to count curves can be refined by the standard Block–Göttsche refined multiplicity to give tropical refined invariants. We then give a concrete algorithm using floor diagrams to compute these invariants along with the associated interpretation as operators acting on some Fock space. The floor diagram algorithm allows one to prove the piecewise polynomiality of the relative invariants, and the quasi-modularity of their generating series.
