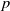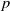1 results
On twisted group ring isomorphism problem for p-groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 368-381
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
In this article, we explore the problem of determining isomorphisms between the twisted complex group algebras of finite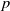
$p$-groups. This problem bears similarity to the classical group algebra isomorphism problem and has been recently examined by Margolis-Schnabel. Our focus lies on a specific invariant, referred to as the generalized corank, which relates to the twisted complex group algebra isomorphism problem. We provide a solution for non-abelian 
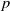$p$-groups with generalized corank at most three.
