We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In 1946, Erdős and Niven proved that no two partial sums of the harmonic series can be equal. We present a generalisation of the Erdős–Niven theorem by showing that no two partial sums of the series
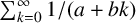$\sum _{k=0}^\infty {1}/{(a+bk)}$
can be equal, where a and b are positive integers. The proof of our result uses analytic and p-adic methods.
