We investigate unramified extensions of number fields with prescribed solvable Galois group G and certain extra conditions. In particular, we are interested in the minimal degree of a number field K, Galois over 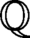 $\mathbb {Q}$
, such that K possesses an unramified G-extension. We improve the best known bounds for the degree of such number fields K for certain classes of solvable groups, in particular for nilpotent groups.
$\mathbb {Q}$
, such that K possesses an unramified G-extension. We improve the best known bounds for the degree of such number fields K for certain classes of solvable groups, in particular for nilpotent groups.
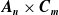 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields