1 results
Optimal stopping on trajectories and the ballot problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 946-959
- Print publication:
- December 2001
-
- Article
- Export citation
-
An urn contains m minus balls and p plus balls, and we draw balls from this urn one at a time randomly without replacement until we wish to stop. Let Pn and Mn denote the respective numbers of plus balls and minus balls drawn by time n and define Z0 = 0, Zn = Pn - Mn, 1 ≤ n ≤ m + p. The main problem of this paper is to stop with maximum probability on the maximum of the trajectory formed by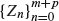
. This problem is closely related to the celebrated ballot problem, so that we obtain some identities concerning the ballot problem and then derive the optimal stopping rule explicitly. Some related modifications are also studied.
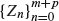. This problem is closely related to the celebrated ballot problem, so that we obtain some identities concerning the ballot problem and then derive the optimal stopping rule explicitly. Some related modifications are also studied.