1 results
To the dynamics of the two-body problem with variable masses in the presence of reactive forces
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 17 / Issue S370 / August 2021
- Published online by Cambridge University Press:
- 16 August 2023, pp. 281-282
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
-
We studied the problem of two spherical celestial bodies in the general case when the masses of the bodies change non-isotropically at different rates in the presence of reactive forces. The problem was investigated by methods of perturbation theory based on aperiodic motion along a quasi-conic section, using the equation of perturbed motion in the form of Newton’s equations. The problem is described by the variables a, e, i, π, ω, λ, which are analogs of the corresponding Keplerian elements and the equations of motion in these variables are obtained. Averaging over the mean longitude, we obtained the evolution equations of the two-body problem with variable masses in the presence of reactive forces. The obtained evolution equations have the exact analytic integral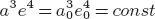
${a^3 e^4 = a^3_0 e^4_0} = {const}$.
